Using Global Satellite Data to Predict Consumption in Ghana
knitr::opts_chunk$set(echo = TRUE, warning = FALSE)
rm(list=ls())
list.of.packages = c('knitr','broom','boot','ggplot2','magrittr','kableExtra','papeR','stargazer')
new.packages = list.of.packages[!(list.of.packages %in% installed.packages()[,"Package"])]
if(length(new.packages)) install.packages(new.packages)
for(package in list.of.packages){
library(package, character.only = T)
}
rm(list=c('list.of.packages','new.packages','package'))
All datasets for this notebook can be found at https://www.kaggle.com/tnightengale/using-global-satellite-data-in-ghana/data. This notebook can also be viewed on kaggle.com at https://www.kaggle.com/tnightengale/using-global-satellite-data-in-ghana.
# set dataset pathways
dat.LSMS = '/Users/tnightengale/Desktop/Kaggle/Kiva/LSMS/GHA_2009_GSPS_v01_M_CSV/Consumption\ Aggregates_CSV/percapita_expenditure.csv'
dat.AID = '/Users/tnightengale/Desktop/Kaggle/Kiva/Aid\ Data/ghana/aid_data_ghana.csv'
dat.Kiva_mpi = '/Users/tnightengale/Desktop/Kaggle/Kiva/data-science-for-good-kiva-crowdfunding/kiva_mpi_region_locations.csv'
dat.burk = '/Users/tnightengale/Desktop/Kaggle/Kiva/Aid\ Data/burkina_district/5afa5909c15e0052b7badaef_results.csv'
Introduction
Kiva is a non-profit organiztion that seeks to connect economically underdeveloped communities with micro-loans. Currently, Kiva does not have the organizational reach to manually assess the financial need of loan applicants. Loans are typically applied for online, and distributed through local partners. Kiva would like to be able to predict the financial need of applicants, but the data they have is limited. Kiva primarily relies on the Multidimensional Poverty Index (MPI), a cross-dimensional measure of well-being developed by Alkire and Foster (2011) in conjunction with The Oxford Poverty and Human Development Initiative. The MPI measure is decomposible by region in most countires, but this implies that the best estimate of an applicant’s well-being is their location within a sub-national region. This implies that Kiva is looking for new granular datasets, that can be used to model the financial-need of an applicant on a sub-regional level. Indeed,
An ideal data source for understanding poverty or financial inclusion in a region would be granular, global, and accurate. It may not surprise you to hear that there is no such dataset. But there are data sources that hit any two of those points. For example, a World Bank Living Standards survey is localized and granular whereas the MPI and Global Findex datasets are global and not granular. - Elliot Collins, Kiva Impact Team
Kiva and kaggle.com recently posed this problem to the Kaggle data science community. I eschew the conventional process of exploring the datasets provided by Kiva to focus on implementing a combination of external datasets to demonstrate how district level data can be utilized to model financial need at a sub-regional level below that detailed by MPI. I utilize granular district data for the country of Ghana obtained from a 2010 Living Standards Measurment Survey (LSMS) in conjunction with a compliation dataset of hard-coded geographical features to generate a district level model of financial need. The geo-data compilation is curated by Aid Data, a research lab at William and Mary College in Virgina. The Aid Data portal provides independently collected geographical variables such as distance to water, cities, other borders, light levels, and roads, on a sub-regional level, and is globally available. This notebook demonstrates how the globally available geographical Aid Data compliation might be used to predict financial need at the district level of granularity.
Datasets
I begin by loading the 2010 Ghanian LSMS data and converting the interger district codes into a factor variable with the names of the district. The pdf documentation accompanying the LSMS data is too poorly formatted to be parsed effectively. Therefore, I manually create a list of district names from the LSMS documentation, using the Aid Data district names as reference. Although this is an unfortunate and relatively time-intensive task, it is likely not necessary for other LSMS datasets. The LSMS datasets are a collection of independent datasets: therefore the quality of documentation and label encoding differs between sets.
To mitigate the loss of matched districts between the Aid Data compilation and and the LSMS data, I judicially extend the Aid Data district labels to some of the more highly differentiated lablels found in the LSMS data. For example, the LSMS data differentiates ‘Ketu North’ and ‘Ketu South’ as distinct districts, whereas the Aid Data refers only to the collective ‘Ketu’ district.
lsms_ghana = read.csv(dat.LSMS)
# manual list of districts from the accompanying documentation and with reference to the Aid Data districts
districts = c('Ahanta West','Aowin Suaman','Bia','Bibiani Anhwiaso Bekwai','Ellembele','Jomoro','Juabeso','Mpohor Wassa East','Nzema East','Prestea Huni Valley','Sefwi Akontobra','Sefwi Wiawso','Sekondi Takoradi','Shama Ahanta East','Tarkwa Nsuaem','Wasa Amenfi East','Wasa Amfenfi West','Abura-Asebu-Kwamankese','Agona','Agona','Ajumako-Enyan-Esiam','Asikuma Odoben Brakwa','Assin North','Assin South','Awutu Efutu Senya','Cape Coast','Awutu Efutu Senya','Gomoa','Gomoa','Komenda-Edina-Eguafo-Abirem','Mfantsiman','Lower Denkyira','Upper Denkhira','Upper Denkhira','Accra','Adenta','Ashaiman','Dangbe East','Dangbe West','Ga East','Ga West','Ledzekuku-Krowor','Tema','Weija','Adaklu Anyigbe','Akatsi','Biakoye','Ho','Hohoe','Jasikan','Kadjebi','Keta','Ketu','Ketu','Kpandu','Krachi East','Krachi West','Nkwanta','Nkwanta','North Tongu','South Tongu','South Dayi','Akwapim North','Akwapim South','Akyemansa','Asuogyaman','Atiwa','Birim North','Birim North','Birim South','East Akim','Fanteakwa','Kwabibirem','Kwahu East','Afram Plains','Kwahu South','Kwahu West','Manya Krobo','New Juaben','Suhum Kraboa Coaltar','Manya Krobo','West Akim','Yilo Krobo','Adansi North','Adansi South','Afigya Sekyere','Ahafo Ano North','Ahafo Ano South','Amansie Central','Amansie East','Amansie West','Asante Akim North','Asante Akim South','Atwima Mponua','Atwima','Atwima','Bekwai','Bosome Freho','Bosomtwe-Kwanwoma','Ejisu-Juabeng','Ejura Sekyedumase','Kumasi','Kwabre','Mampong','Obuasi Municipal','Offinso','Offinso','Sekyere West','Sekyere West','Sekyere East','Sekyere West','Asunafo North','Asunafo South','Asutifi','Atebubu-Amantin','Berekum','Dormaa','Dormaa','Jaman North','Jaman South','Kintampo North','Kintampo South','Nkoranza','Nkoranza','Pru','Sene','Sunyani','Sunyani','Tain','Tano North','Tano South','Techiman','Wenchi','Bole','Bunkpurugu Yunyoo','Central Gonja','Saboba Chereponi','East Gonja','East Mamprusi','Gushiegu','Karaga','Kpandai','Nanumba North','Nanumba South','Saboba Chereponi','Savelugu Nanton','Sawa-Tuna-Kalba','Tamale','Tolon-Kumbungu','West Gonja','West Mamprusi','Yendi','Zabzugu Tatale','Bawku Municipal','Bawku West','Bolgatanga','Bongo','Builsa','Garu Tempane','Kassena Nankana','Kassena Nankana','Talensi Nabdam','Jirapa Lambussie','Jirapa Lambussie','Lawra','Nadowli','Sissala East','Sissala West','Wa','Wa East','Wa West')
# encode the districts mannually as the documentation cannot be parsed
lsms_ghana = na.omit(lsms_ghana)
dstr_levels = sort(unique(lsms_ghana$id2))
dstr_labels = districts[dstr_levels]
dstr_dupl = which(duplicated(dstr_labels))
for(i in 1:length(dstr_dupl)){
lsms_ghana$id2[which(lsms_ghana$id2 == dstr_levels[dstr_dupl[i]])] <- dstr_levels[dstr_dupl[i]-1]
}
dstr_labels = dstr_labels[-dstr_dupl]
dstr_levels = dstr_levels[-dstr_dupl]
lsms_ghana$id2 = factor(lsms_ghana$id2, levels = dstr_levels, labels = dstr_labels)
#rm(list = ls()[-which(ls() == 'lsms_ghana')])
lsms_ghana$id1 = factor(lsms_ghana$id1, labels = c('Western','Central','Greater Accra','Volta','Eastern','Ashanti','Brong Ahafo','Northern','Upper East','Upper West'))
lsms_ghana = lsms_ghana[which(colnames(lsms_ghana) %in% c('id1','id2','avg_s11_monthly_exp','percapita_exp'))]
colnames(lsms_ghana) = c('Region','District','hh_avg_mnthly_expend','hh_per_cap_mnthly_expend')
Regional MPI is a comprehensive indicator of financial need, based on a variety of aggregated poverty dimensions. The goal of this investigation is to attempt to develop a model that is able to predict the financial need of loan applicants at the sub-regional level. Therefore, any potential sub-regional measure of financial need should be correlated with regional MPI, if we hope to use the sub-regional measure to build a meaningful model.
I consider two sub-regional measures of financial need from the LSMS dataset: average monthly household consumption expenditures and average monthly per-capita consumption expenditures. All values are assumed to be in 2010 USD, as the LSMS documentation does not specify otherwise. Consumption expenditures encompass the total amount used to purchase any good, and thus includes funds spent on food, transportation, education, etc. It seems likely that one of these measure might be a good substitute for regional MPI for the purposes of evaluating financial need.
I now average across households in the LSMS data to calculate average
monthly household expenditure and average per capita expenditure on a
per district basis. I compare this measure with the Ghanaian regional
MPI measure provided in the kiva_mpi dataset. By comparing 2010 LSMS
consumption measures with more recent regional MPI measues, we are
implicitly assuming that Ghanaian consumption has stayed reasonably
constant over time.
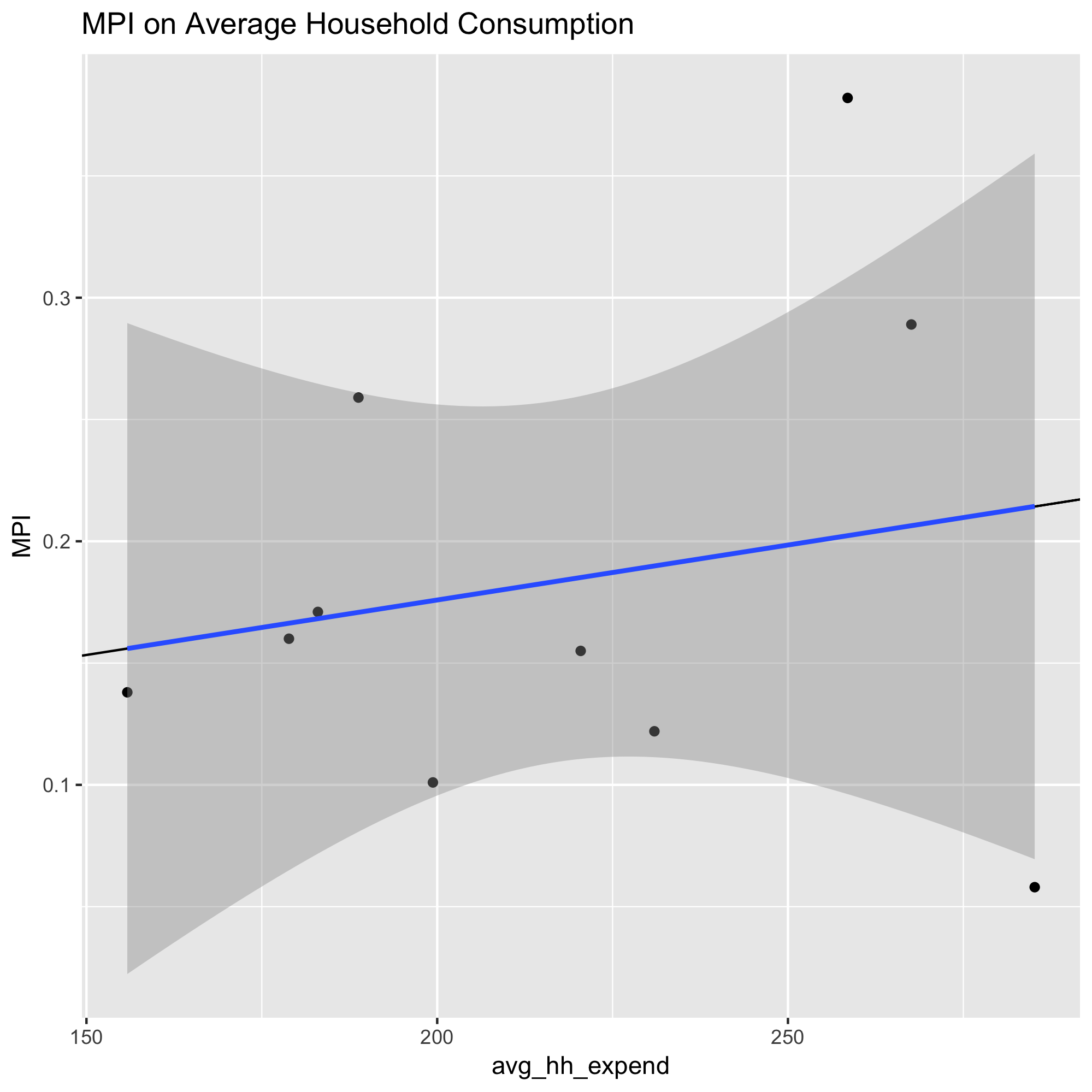
Below are the results of an OLS estimation of regional MPI on regional average monthly household expenditure.

| Dependent variable: | |
| MPI | |
| avg\_hh\_expend | 0.0005 |
| (0.001) | |
| Constant | 0.086 |
| (0.174) | |
| Observations | 10 |
| R2 | 0.039 |
| Adjusted R2 | -0.081 |
| Residual Std. Error | 0.102 (df = 8) |
| F Statistic | 0.327 (df = 1; 8) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
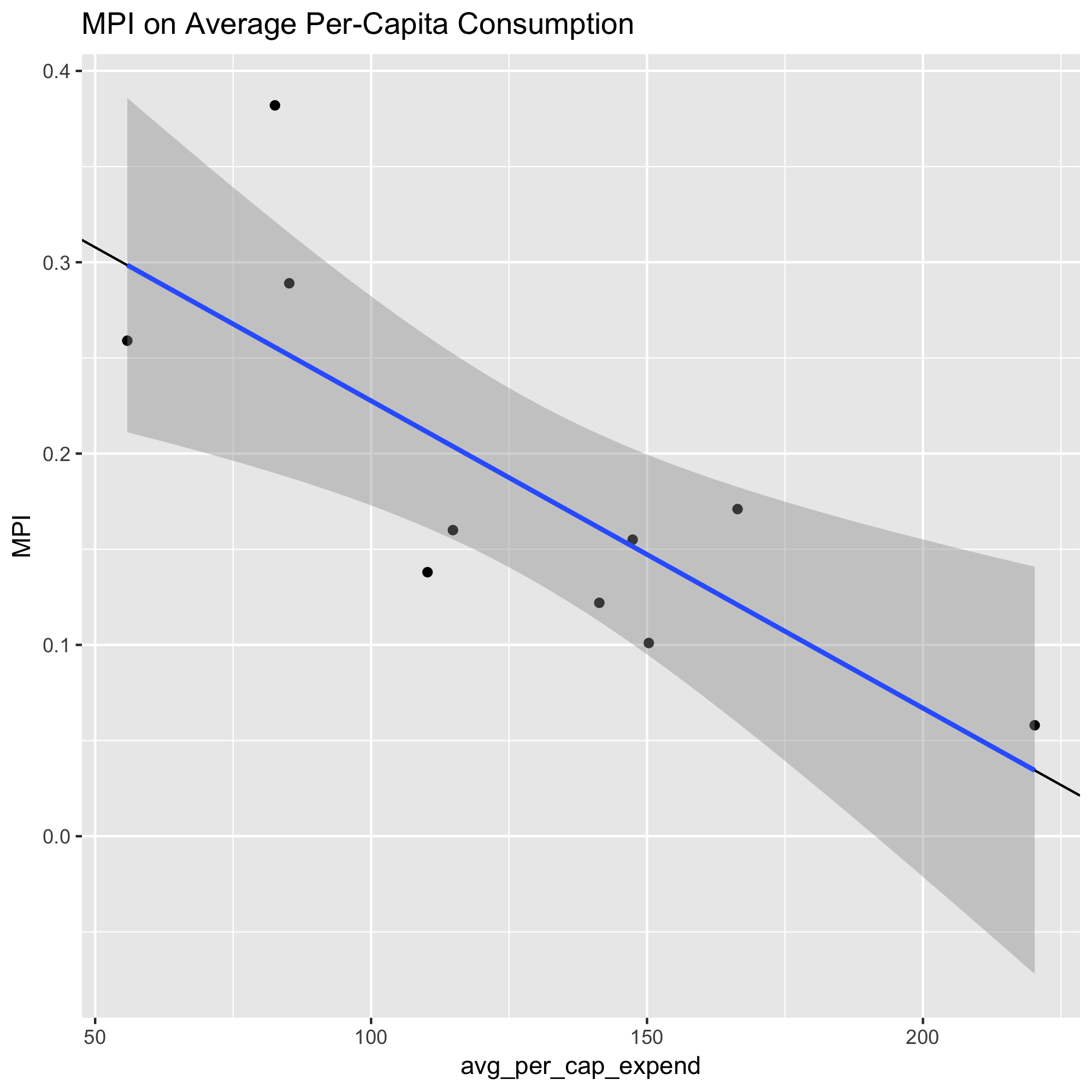
The OLS estimation shows regional average monthly household expenditure to be a poor approximation for regional MPI. So I turn to the alternative measure of average per capita expenditure.

| Dependent variable: | |
| MPI | |
| avg\_per\_cap\_expend | -0.002\*\*\* |
| (0.0004) | |
| Constant | 0.388\*\*\* |
| (0.060) | |
| Observations | 10 |
| R2 | 0.618 |
| Adjusted R2 | 0.570 |
| Residual Std. Error | 0.064 (df = 8) |
| F Statistic | 12.930\*\*\* (df = 1; 8) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
In contrast, average per capita consumption appears to be a reasonable substitue for regional MPI. Note that a MPI of 1 indicates deprivation, which is defined as a level below a subjective poverty cutoff, across every dimension of the index. Hence the negative relationship to per-capita expenditures.
Now I load the Aid Data compilation containing hardcoded geographical feature data and match it to the LSMS using district names. The table below contains a summary of the features present in the compilation. Note that there are other geographical variables available on a global scale from the Aid Data portal. The compilation I am using is simply a mixture of independent dataset I choose from the portal because I thought they have predictve potential.
raster_ghana = read.csv(dat.AID)
colnames(raster_ghana) = c('asdf_id','sum_aid_1995-2014','light_composite_index_count','light_composite_index_mean','avg_precip_mm','conflict_deaths','veg_index','d','avg_pop_dens_km^2','max_pop_dens_km^2','d','IPPC_total_count','IPPC_cropland','IPPC_rainfed_cropland','IPPC_shrubland','IPPC_urban','IPPC_water','IPPC_forest','d','IPPC_bare','IPPC_sparse_veg','IPPC_grassland','IPPC_wetland','IPPC_irrigated','IPPC_snow','dist_coast_max','d','dist_coast_avg','dist_coast_min','dist_water_avg','dist_water_max','dist_water_min','dist_road_avg','dist_road_max','d','dist_border_avg','dist_border_max','dist_border_min','child_mortality_per1000','ACLED_conflit_count','d','d','travel_to_city_avg_mins','travel_to_city_max_mins','travel_to_city_min_mins','District','d','Region','d','Metropolian_categorical','shape_area','d','shape_length','HASC_2','d','d','d','d','d','d','d')
raster_ghana = raster_ghana[-which(colnames(raster_ghana) == 'd')]
district_averages = data.frame(as.vector(with(lsms_ghana, tapply(hh_avg_mnthly_expend, District, mean))), as.vector(with(lsms_ghana, tapply(hh_per_cap_mnthly_expend, District, mean))), levels(lsms_ghana$District))
colnames(district_averages) = c('avg_hh_monthly_expend','avg_per_cap_monthly_expend','District')
ghana_merge = merge(district_averages,raster_ghana, by = 'District')
stargazer(raster_ghana,type = 'html',title='Summary of Aid Data Compilation',align=T)
| Statistic | N | Mean | St. Dev. | Min | Max |
| asdf\_id | 137 | 68.000 | 39.693 | 0 | 136 |
| sum\_aid\_1995-2014 | 137 | 42,627,767.000 | 33,936,731.000 | 6,134,710.000 | 198,578,848.000 |
| light\_composite\_index\_count | 137 | 2,068.546 | 2,014.587 | 152.730 | 11,689.160 |
| light\_composite\_index\_mean | 137 | 2.373 | 7.460 | 0.000 | 60.780 |
| avg\_precip\_mm | 135 | 100.999 | 16.413 | 63.442 | 143.477 |
| conflict\_deaths | 137 | 0.058 | 0.683 | 0 | 8 |
| veg\_index | 137 | 5,226.019 | 895.561 | 2,583.599 | 6,541.908 |
| avg\_pop\_dens\_km2 | 137 | 286.311 | 876.566 | 10.455 | 7,629.113 |
| max\_pop\_dens\_km2 | 137 | 916.105 | 2,156.585 | 38.289 | 11,258.440 |
| IPPC\_total\_count | 137 | 18,497.690 | 18,074.600 | 1,336 | 104,723 |
| IPPC\_cropland | 137 | 1,976.182 | 2,411.668 | 3 | 15,955 |
| IPPC\_rainfed\_cropland | 137 | 6,730.686 | 4,402.073 | 53 | 24,334 |
| IPPC\_shrubland | 137 | 2,573.547 | 5,274.287 | 0 | 23,016 |
| IPPC\_urban | 137 | 149.504 | 373.105 | 0 | 2,734 |
| IPPC\_water | 137 | 508.985 | 1,981.069 | 0 | 15,573 |
| IPPC\_forest | 137 | 6,530.788 | 13,639.000 | 0 | 79,422 |
| IPPC\_bare | 137 | 2.869 | 14.749 | 0 | 157 |
| IPPC\_sparse\_veg | 137 | 0.197 | 1.392 | 0 | 14 |
| IPPC\_grassland | 137 | 3.161 | 8.961 | 0 | 58 |
| IPPC\_wetland | 137 | 8.073 | 61.766 | 0 | 587 |
| IPPC\_irrigated | 137 | 13.701 | 56.622 | 0 | 441 |
| IPPC\_snow | 137 | 0.000 | 0.000 | 0 | 0 |
| dist\_coast\_max | 137 | 245,953.900 | 190,339.100 | 16,184.400 | 657,565.200 |
| dist\_coast\_avg | 137 | 219,219.000 | 184,509.700 | 7,360.971 | 623,982.400 |
| dist\_coast\_min | 137 | 192,108.700 | 178,485.400 | 0.000 | 591,204.900 |
| dist\_water\_avg | 137 | 45,888.240 | 37,141.820 | 1,824.964 | 138,690.200 |
| dist\_water\_max | 137 | 68,498.200 | 38,987.930 | 8,923.586 | 155,688.500 |
| dist\_water\_min | 137 | 26,142.890 | 33,842.290 | 0.000 | 120,700.900 |
| dist\_road\_avg | 137 | 3,123.644 | 1,389.788 | 1,258.858 | 9,427.666 |
| dist\_road\_max | 137 | 11,102.670 | 4,595.444 | 4,956.516 | 26,599.400 |
| dist\_border\_avg | 137 | 61,401.150 | 47,889.230 | 2,764.334 | 171,264.200 |
| dist\_border\_max | 137 | 85,774.040 | 50,402.160 | 11,552.110 | 191,333.500 |
| dist\_border\_min | 137 | 39,011.260 | 44,473.560 | 0.000 | 148,783.400 |
| child\_mortality\_per1000 | 136 | 20.368 | 6.639 | 7.555 | 35.061 |
| ACLED\_conflit\_count | 137 | 1.773 | 5.974 | 0.000 | 57.840 |
| travel\_to\_city\_avg\_mins | 137 | 185.823 | 97.265 | 10.713 | 548.577 |
| travel\_to\_city\_max\_mins | 137 | 522.818 | 235.870 | 52 | 1,316 |
| travel\_to\_city\_min\_mins | 137 | 51.409 | 50.570 | 0 | 217 |
| shape\_area | 137 | 0.143 | 0.139 | 0.010 | 0.808 |
| shape\_length | 137 | 1.783 | 0.886 | 0.503 | 6.654 |
Unfortunately, not all the district labels present in the LSMS dataset align with district labels in the Aid Data, due to differing naming conventions and a lack of sufficient overlapping data. The resulting merged dataset of average monthly household expenitures and geographic featues is limited to 94 districts.
Analysis
To account for the small sample size of viable districts I utilize several simple MLS models with limited dependent variables to predict district level per captia income for 94 of Ghana’s districts. I build a simple leave one out cross validation (LOOCV) algorithm to evaluate the cross-validated mean squared error (CV-MSE) for several specifications.
LOOCV = function(df,fm,dep_col){
# takes in a dataframe, a call formula
# (y~x1+x2...), and the column index of
# the dependent variable (y) to return
# the average of the MSE's, where each
# MSE is calculated using the predicted
# and true values of holdout observation i
MSE_grid = rep(0,nrow(df))
for(i in 1:nrow(df)){
temp_df = df[-i,]
temp_obs = df[i,]
model = lm(fm, data = temp_df)
prediction = predict.lm(model, newdata = temp_obs)
MSE_i = (prediction - df[i,dep_col])^2
MSE_grid[i] = MSE_i
}
return(mean(MSE_grid))
}
Index Models
Model 1 uses two indices from the Aid Data to attempt to predict
average per-capita consumption expenditures by district. The first index
is callibrated measure of persistent light, constructed by the NOAA
National Geophysical Data Center using satellite images collected by the
US Air Force Weather Agency. The second is the Normalized Difference
Vegetation Index (NDVI), created by Pedelty, Devadiga, Masuoka et al.
(2007) using the data from the NASA Long Term Data Record. I first run a
simple MLS estimation of the two index model using a level-level
specification and find a CV-MSE of 1862. However, the level-log
specification of Model 2 yields a lower CV-MSE of 1585 and provides a
more reasonable interpretation when working with arbitrary indicies: a
percentage increase (decrease) in the NOAA light index, relative to the
mean index value for all of Ghana predicts an increase (decrease) of
approximately $15 USD (2010) in monthly consumption.
index_data = ghana_merge[c(3,7,10)]
# level-level model_1
model_1 = lm(avg_per_cap_monthly_expend~., data = index_data)
cv.mse.1 = LOOCV(index_data,model_1$call,1)
# level-log transformation
log_index_data = index_data[-which(index_data$light_composite_index_mean == 0),]
log_index_data[2] = log(log_index_data[2])
log_index_data[3] = log(log_index_data[3])
# level-log index model_2
model_2 = lm(avg_per_cap_monthly_expend~light_composite_index_mean+veg_index, data = log_index_data)
cv.mse.2 = LOOCV(log_index_data,model_2$call,1)
Model 3 and Model 4 use only the light index in a level-level and
level-log specification respectively. The CV-MSE for each of the models
are presented in the table below.
# model_3
model_3 = lm(avg_per_cap_monthly_expend~light_composite_index_mean, data = index_data)
cv.mse.3 = LOOCV(index_data,model_3$call,1)
# model_4
model_4 = lm(avg_per_cap_monthly_expend~light_composite_index_mean, data = log_index_data)
cv.mse.4 = LOOCV(log_index_data,model_4$call,1)
Below is a summary of the CV-MSE for each of the models specified above.
stargazer(model_1,model_2,model_3,model_4,type='html',title = 'Models 1-4')
| Dependent variable: | ||||
| avg\_per\_cap\_monthly\_expend | ||||
| (1) | (2) | (3) | (4) | |
| light\_composite\_index\_mean | 4.612\*\*\* | 15.159\*\*\* | 3.846\*\*\* | 14.984\*\*\* |
| (0.714) | (2.014) | (0.732) | (2.034) | |
| veg\_index | 0.019\*\*\* | 40.188\* | ||
| (0.005) | (23.338) | |||
| Constant | 0.384 | -213.931 | 101.098\*\*\* | 129.649\*\*\* |
| (27.041) | (199.585) | (4.793) | (4.810) | |
| Observations | 94 | 89 | 94 | 89 |
| R2 | 0.335 | 0.405 | 0.231 | 0.384 |
| Adjusted R2 | 0.320 | 0.391 | 0.222 | 0.377 |
| Residual Std. Error | 41.110 (df = 91) | 38.875 (df = 86) | 43.973 (df = 92) | 39.311 (df = 87) |
| F Statistic | 22.928\*\*\* (df = 2; 91) | 29.228\*\*\* (df = 2; 86) | 27.612\*\*\* (df = 1; 92) | 54.265\*\*\* (df = 1; 87) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 | |||
CV-MSE by Model Specification
kable(data.frame(cv.mse.1,cv.mse.2,cv.mse.3,cv.mse.4), format = 'markdown', col.names = c('Model 1','Model 2','Model 3','Model 4'))
| Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|
| 1861.865 | 1585.381 | 2052.783 | 1588.147 |
Bootstrap
Model 2 has the lowest CV-MSE and this implies that the average
standard error (the square root of the MSE) of the model is $39.82 USD.
Let’s bootstrap the standard errors on Model 2 specification to assess
the robustness of the model.
boot.fn = function(data, index){
a = coef(lm(formula = log_index_data$avg_per_cap_monthly_expend ~ log_index_data$light_composite_index_mean + log_index_data$veg_index, data = data, subset = index))
return(a)
}
boot.fn(log_index_data ,sample (89 ,89 , replace =T))
## (Intercept)
## -8.639082
## log_index_data$light_composite_index_mean
## 15.269948
## log_index_data$veg_index
## 16.345364
bootstraps = boot(log_index_data,boot.fn,1000)
bootstraps
##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = log_index_data, statistic = boot.fn, R = 1000)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* -213.93071 -7.43908931 216.825114
## t2* 15.15938 -0.07465064 2.308033
## t3* 40.18765 0.85261006 25.166084
The bootstrapped standard errors on the indices appear to be reasonably
close to the estimated standard errors of Model 2 reported earlier.
Land Proportion Models
The Aid Data compilation contains other types of hardcoded data including counts of UN Land Cover Classification System (LCCS) terrain classes. The LCCS features are counts of different land types within each district. The Eupopean Space Agency (ESA) provides the satellite images which are decomposed into samples tiling the district of interest. Each tile is classified by the ESA into a LCCS category of terrain. The tiles are assumed to be uniform size between districts, and the district-specific count of all terrian categories is the number of tiles covering the district of interest.
I standardize the different counts of terrain tiles present for each district, by converting each count to a ratio, to create a proportional terrain type model. The results of an MLS estimation of the model are presented below.
prop_data = ghana_merge[c(2,13:23)]
prop_data[2:ncol(prop_data)] = prop_data[2:ncol(prop_data)]/ghana_merge$IPPC_total_count
prop_model = lm(avg_hh_monthly_expend~.-IPPC_total_count, data = prop_data)
stargazer(prop_model, type = 'html', title = 'Proportional Land Type Model MLS Estimation')
| Dependent variable: | |
| avg\_hh\_monthly\_expend | |
| IPPC\_cropland | -605.753 |
| (2,067.483) | |
| IPPC\_rainfed\_cropland | -667.919 |
| (2,068.242) | |
| IPPC\_shrubland | -551.671 |
| (2,075.431) | |
| IPPC\_urban | -197.513 |
| (2,096.749) | |
| IPPC\_water | -910.391 |
| (2,081.144) | |
| IPPC\_forest | -648.913 |
| (2,067.200) | |
| IPPC\_bare | 22,653.180 |
| (27,944.270) | |
| IPPC\_sparse\_veg | -236,084.400 |
| (258,394.900) | |
| IPPC\_grassland | -19,403.650\*\* |
| (9,543.027) | |
| IPPC\_wetland | 17,773.340 |
| (16,035.920) | |
| Constant | 840.746 |
| (2,067.910) | |
| Observations | 94 |
| R2 | 0.372 |
| Adjusted R2 | 0.296 |
| Residual Std. Error | 64.797 (df = 83) |
| F Statistic | 4.917\*\*\* (df = 10; 83) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
# check CV-MSE:
kable(LOOCV(prop_data,prop_model$call,1), col.names = 'LOOCV-MSE', align = 'left')
| LOOCV-MSE |
|---|
| 14902.43 |
Clearly this model does not compare to the index model on the basis of MSE.
Distance Models
The Aid Data compilation also contains distance statistics for features such as roads and water. I again create a linear model containing these features. The results of an MLS estimation of the distance model are presented below.
distance_data = ghana_merge[c(2,26:35)]
# convert to km
distance_data[2:ncol(distance_data)] = distance_data[2:ncol(distance_data)]/1000
distance_model = lm(avg_hh_monthly_expend~., data = distance_data)
#kable(prettify(summary(distance_model)))
stargazer(distance_model, type = 'html', title = 'Distance Model MLS Estimation')
| Dependent variable: | |
| avg\_hh\_monthly\_expend | |
| dist\_coast\_max | 0.455 |
| (1.581) | |
| dist\_coast\_avg | -2.260 |
| (2.861) | |
| dist\_coast\_min | 1.880 |
| (1.569) | |
| dist\_water\_avg | 1.571 |
| (2.469) | |
| dist\_water\_max | -1.524 |
| (1.584) | |
| dist\_water\_min | -0.191 |
| (1.402) | |
| dist\_road\_avg | -7.709 |
| (14.031) | |
| dist\_road\_max | 4.679 |
| (5.293) | |
| dist\_border\_avg | -1.405 |
| (1.474) | |
| dist\_border\_max | 1.337 |
| (1.508) | |
| Constant | 202.455\*\*\* |
| (29.593) | |
| Observations | 94 |
| R2 | 0.083 |
| Adjusted R2 | -0.028 |
| Residual Std. Error | 78.319 (df = 83) |
| F Statistic | 0.747 (df = 10; 83) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
The distance model fits so poorly under the current specification, that I do not bother calculating MSE. It would be interesting to extend this data to further models, to determine if these features offer any predicative capabilities within other frameworks. The Aid Data compilation used in this kernel can be found under the data section. Links to the data resources used in this kernel are also provided in the Referrences section. The Aid Data repository is a very interesting collection of hard coded geographical data that may be useful to members of the Kaggle community.
Comparision with Regional MPI Measure
I now return to Model 2 to explore it’s feasibility as a predictor of
financial need.
How well does Model 2 predict regional per-capita consumption and the
regional MPI found in the kiva_mpi dataset? This question is
meaningful because we would like to have some idea of how well our
simple index model relates to Kiva’s provided measures of MPI. To relate
district-level per-capita consumption to the regional-level MPI provided
by Kiva requires two steps. First, I average our predicted
district-level per-capita consumption expenditures by region. Next I use
these predicted regional-level per-capita consumption expenditures to
predict regional MPI and compare the predictions to the regional MPI
measures provided in the Kiva dataset.
# # clean up global enviroment
# rm(list=setdiff(ls(),c('model_2','per_cap_model','LOOCV','ghana_merge','regional_averages')))
# let's astart with predicting regional per-capita by partritioning ghana_merge
# and keeping per-cap, light index, veg index and region
test = ghana_merge[c(3,7,10,42)]
# drop light indices of 0 to get 89 observations == 89 fitted values
test = test[-which(test$light_composite_index_mean == 0),]
# district pre-capita training MSE
dist_MSE = mean((test$avg_per_cap_monthly_expend - model_2$fitted.values)^2)
# add predicted values to model 2
test = cbind(test,model_2$fitted.values)
colnames(test) = c(colnames(test)[1:4],'per_cap_predict')
# average across regions
test = data.frame(as.vector(with(test, tapply(avg_per_cap_monthly_expend, Region, mean))),as.vector(with(test, tapply(per_cap_predict, Region, mean))), levels(test$Region))
colnames(test) = c('avg_per_cap_monthly_expend','per_cap_predict','region')
# regional per-capita training MSE
reg_MSE = mean((test$avg_per_cap_monthly_expend - test$per_cap_predict)^2)
kable(data.frame(cv.mse.2,dist_MSE,reg_MSE), format = 'markdown', col.names = c('Model 2 LOOCV MSE','District-Level Training MSE','Regional-Level MSE'), caption = 'This is a comment')
| Model 2 LOOCV MSE | District-Level Training MSE | Regional-Level MSE |
|---|---|---|
| 1585.381 | 1460.311 | 368.5719 |
# kable(data.frame(dist_MSE,reg_MSE), col.names = c('District Training MSE','Region Training MSE'))
The district-level training MSE of 1460 is lower than the CV-MSE of 1585, which is to be expected. However the regional-level training MSE of 369 is much lower than the district-level 1460. This implies that the model does a relatively good job of predicting average per-capita expenditures on the regional-level.
How well does the model predict regional MPI using predicted region-average per-capita expenditures?
# merge with regional averages to compare to Kiva MPI values
test = merge(test,regional_averages, by = c('region'))
# create a level-level OLS estimation of MPI using true regional average consumption expenditues
temp_data = data.frame(test$per_cap_predict)
colnames(temp_data) = 'avg_per_cap_expend'
temp_model = lm(MPI~avg_per_cap_expend,data=test)
# predict regional MPI using our earlier prediction of regional average consumption expenditures, and add to the test dataframe
predict(temp_model,temp_data)
## 1 2 3 4 5 6 7
## 0.1761529 0.2184376 0.1755690 0.1877576 0.1566138 0.2627779 0.2443662
## 8 9 10
## 0.2816503 0.1996626 0.2014263
test = cbind(test,predict(temp_model,temp_data))
colnames(test) = c(colnames(test)[1:6],'MPI_predict')
stargazer(temp_model,type='html',title = 'MPI on log Predicted Per-Capita Consumption')
| Dependent variable: | |
| MPI | |
| avg\_per\_cap\_expend | -0.002\*\*\* |
| (0.0004) | |
| Constant | 0.388\*\*\* |
| (0.060) | |
| Observations | 10 |
| R2 | 0.618 |
| Adjusted R2 | 0.570 |
| Residual Std. Error | 0.064 (df = 8) |
| F Statistic | 12.930\*\*\* (df = 1; 8) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
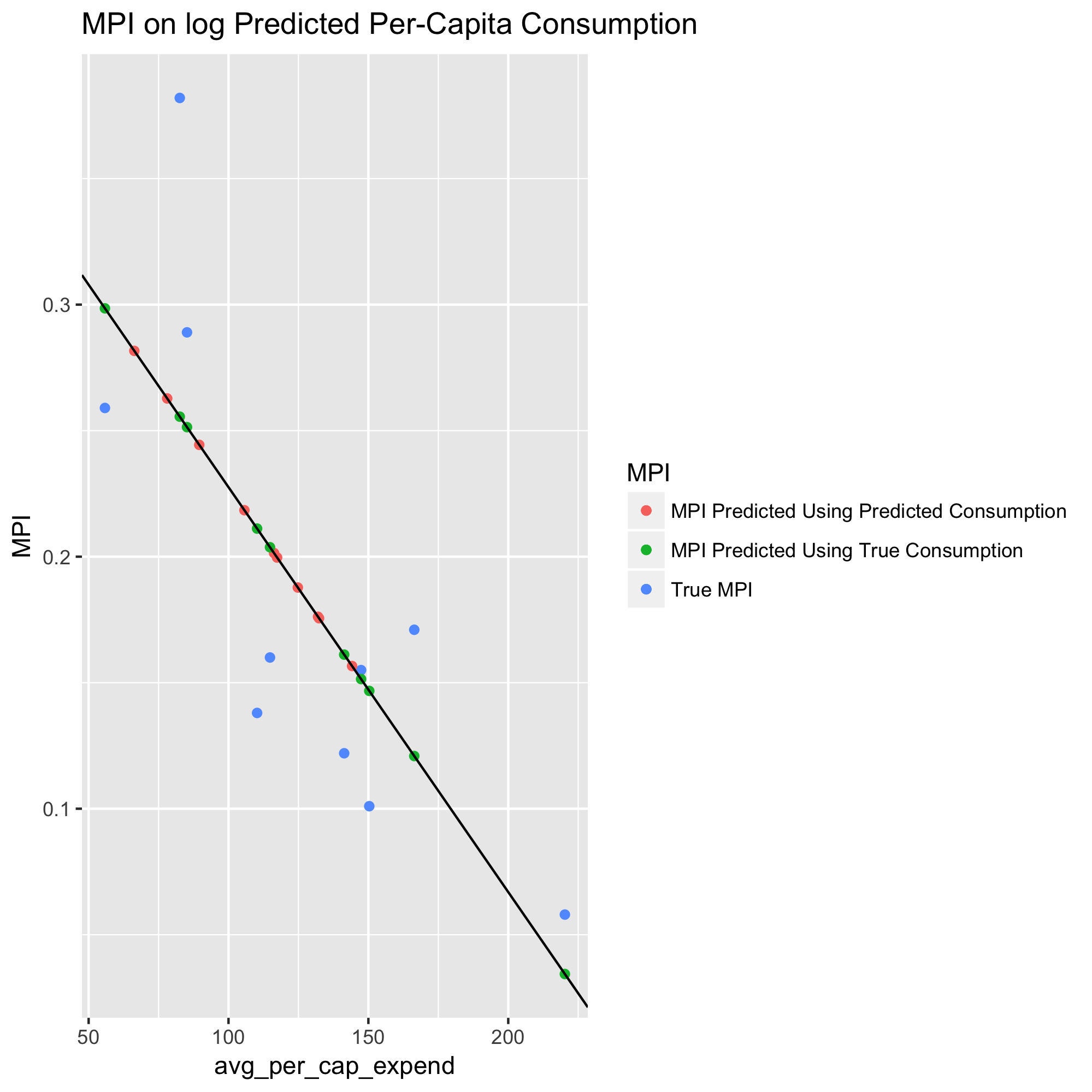
Below is a visualisation of the OLS model presented above.
attach(test)
ggplot(test, aes(avg_per_cap_expend,MPI, colour = 'True MPI')) + geom_point() +
geom_point(aes(per_cap_predict,MPI_predict,colour = 'MPI Predicted Using Predicted Consumption')) +
geom_point(aes(avg_per_cap_expend,temp_model$fitted.values, colour = 'MPI Predicted Using True Consumption')) +
geom_abline(intercept = temp_model$coefficients[1], slope=temp_model$coefficients[2]) +
ggtitle('MPI on log Predicted Per-Capita Consumption') +
guides(colour=guide_legend(title='MPI'))

detach(test)
MPI_RMSE = (mean((test$MPI_predict - test$MPI)^2))^.5
kable(MPI_RMSE, col.names = 'MPI RSME', align = 'left')
| MPI RSME |
|---|
| 0.0683458 |
The RSME of 0.0683 can be interpreted as the standard error of this
two-stage model. The standard errors of the predicted per-capita
consumption expenditures were shown earlier to be quite robust for the
Model 2 OLS estimation. This standard error appears reasonable for
predicting regional MPI on a scale of [0,1].
Conclusions
The purpose of this notebook is to explore the feasibility of using
globally available hardcoded geographical features to predict
sub-regional indicators of financial need. I used Ghana as a
proof-of-concept example for this process because it was one of the
countries with the highest frequency of Kiva loans that also had a
Living Standards Measurement Survey available. The frequency of Kiva
loans was preliminarily examined using the provided Kiva Loans
dataset.
The Ghanian LSMS dataset provides data about per-capita consumption expenditures at the district-level and seems to be a very reasonable proxy for MPI at the regional-level, based on the results of a simple OLS estimation.
Microdata containing per-capita expenditures at the sub-regional level is reasonably available on a global scale outside of the LSMS collection from a variety of sources, as this is one of the most common economic indicators of interest for poverty research.
The globally availabe and relatively granular (sub-regional data is available for all countries) Aid Data collection of geographical features appears to be useful for predicting financial need, indicated in this example by per-capita consumption expenditures.
The models presented in this notebook are intentionally simple, general, and widely applicable to encourage replication for other countries. The second index model, which uses the relative strength of light and vegetation indices between districts, appears to offer the best prediction of per-capita consumption, with a cross-validated RMSE of 40, which implies that the standard error of this predictive model is about $40 USD (2010). When these predicted consumption values are aggregated and used to predict the provided regional-level MPI data, the two-stage model performs reasonably well, with a RMSE of 0.068.
The other geographical features in the Aid Data complilation did prove to applicable for a simple MLS framework. In this sense they are not as easily generalizable as the index models, but may prove upon further investigation.
The purpose of this notebook is to investigate the predicative power of a model utilizing both granular and global data. The emphasis is on simplicity and scalability. To that end, the workflow for the general index model is as follows:
- Find a LSMS or other microdata set containing information on sub-regional consumption expenditures for a given country
- Find the consumption statistic that best predicts regional MPI
- Download the corresponding NOAA National Geophysical Data Center persistent light index and the Normalized Difference Vegetation Index
- Match the datasets on district names. This step is relatively time consuming depending on the quality of the microdata documentation and standarization of district naming conventions
- Use a level-log MLS estimation to predict district level financial need, as approximated by a consumption statistic
- Use the model to make predictions about financial need for neighbouring regions or countries
Extending loans to communities and entrepreneurs who have the greatest financial need is crucial for allevating global poverty. A predicted granular measure of financial need has the potential to offer value as a localized measure of poverty, thus providing a district-level datapoint in addition to Kiva’s regional MPI data point for assessing financial need of potential loan applicants. The model presented in this notebook shows how district-level light index data predicts financial need fairly well, with a cross validated standard error of 39.82.
References
-
Alkire, Sabina, and James Foster. “Understandings and Misunderstandings of Multidimensional Poverty Measurement.” The Journal of Economic Inequality, vol. 9, no. 2, 2011, pp. 289-314.
-
AidData. 2017. WorldBank_GeocodedResearchRelease_Level1_v1.4.2 geocoded dataset. Williamsburg, VA and Washington, DC: AidData. Accessed on 2018/05/07. http://aiddata.org/research-datasets.
-
Center for International Earth Science Information Network - CIESIN - Columbia University. 2016. Gridded Population of the World, Version 4 (GPWv4): Population Density Adjusted to Match 2015 Revision UN WPP Country Totals. Palisades, NY: NASA Socioeconomic Data and Applications Center (SEDAC). http://dx.doi.org/10.7927/H4HX19NJ.
-
Center for International Earth Science Information Network - CIESIN - Columbia University, and Information Technology Outreach Services - ITOS - University of Georgia. 2013. Global Roads Open Access Data Set, Version 1 (gROADSv1). Palisades, NY: NASA Socioeconomic Data and Applications Center (SEDAC). http://dx.doi.org/10.7927/H4VD6WCT. Accessed 08 05 2018.
-
Defourny, P. (2017): ESA Land Cover Climate Change Initiative (Land_Cover_cci): Land Cover Maps, v2.0.7. Centre for Environmental Data Analysis, 7/2017
-
Global Administrative Areas (GADM) http://www.gadm.org Global Administrative Areas (GADM) http://www.gadm.org.
-
Marshall Burke, Sam Heft-Neal, and Eran Bendavid. Understanding variation in child mortality across Sub-Saharan Africa: A spatial analysis. The Lancet Global Health, 2016, Volume 4, Issue 12, e936-e94.
-
Nelson, A. (2008) Estimated travel time to the nearest city of 50,000 or more people in year 2000. Global Environment Monitoring Unit Joint Research Centre of the European Commission, Ispra Italy. Available at http://forobs.jrc.ec.europa.eu/products/gam/
-
NOAA National Geophysical Data Center Source Link https://ngdc.noaa.gov/eog/dmsp/downloadV4composites.html Citation. Image and Data processing by NOAA’s National Geophysical Data Center. DMSP data collected by the US Air Force Weather Agency.
-
Hlavac, Marek (2018). stargazer: Well-Formatted Regression and Summary Statistics Tables.
-
Raleigh, Clionadh, Andrew Linke, Håvard Hegre and Joakim Karlsen. 2010. Introducing ACLED-Armed Conflict Location and Event Data. Journal of Peace Research 47(5) 651-660.
-
Sundberg, Ralph, and Erik Melander, 2013, ‘Introducing the UCDP Georeferenced Event Dataset’, Journal of Peace Research, vol.50, no.4, 523-532 Croicu, Mihai and Ralph Sundberg, 2017, “UCDP GED Codebook version 17.1”, Department of Peace and Conflict Research, Uppsala University
-
Pedelty JA, Devadiga S, Masuoka E et al. (2007) Generating a Long-term Land Data Record from the AVHRR and MODIS Instruments. Proceedings of IGARRS 2007, pp. 1021–1025. Institute of Electrical and Electronics Engineers, NY, USA.
-
Wessel, P., and W. H. F. Smith, A Global Self-consistent, Hierarchical, High-resolution Shoreline Database, J. Geophys. Res., 101, #B4, pp. 8741-8743, 1996.
-
Wessel, P., and W. H. F. Smith, A Global Self-consistent, Hierarchical, High-resolution Shoreline Database, J. Geophys. Res., 101, #B4, pp. 8741-8743, 1996.
-
Willmott, C. J. and K. Matsuura (2001) Terrestrial Air Temperature and Precipitation: Monthly and Annual Time Series (1950 - 1999), http://climate.geog.udel.edu/~climate/html_pages/README.ghcn_ts2.html.